Cách nội suy lãi suất|đầu tư

ETFFIN >> Tài chính cá nhân > >> Personal finance >> đầu tư

Cách nội suy lãi suất

Nội suy tuyến tính ước tính giá trị giữa các điểm dữ liệu.

Nội suy là một quá trình toán học để ước tính giá trị của một biến phụ thuộc dựa trên các giá trị của các biến phụ thuộc xung quanh đã biết, trong đó biến phụ thuộc là một hàm của một biến độc lập. Nó được sử dụng để xác định lãi suất cho các khoảng thời gian không được công bố hoặc có sẵn. Trong trường hợp này, lãi suất là biến phụ thuộc và độ dài thời gian là biến độc lập. Để nội suy lãi suất, bạn sẽ cần lãi suất trong một khoảng thời gian ngắn hơn và một khoảng thời gian dài hơn.

Bước 1

Trừ lãi suất của khoảng thời gian ngắn hơn khoảng thời gian có lãi suất mong muốn với lãi suất của khoảng thời gian dài hơn khoảng thời gian có lãi suất mong muốn. Ví dụ:nếu bạn đang nội suy lãi suất 45 ngày và lãi suất 30 ngày là 4,2242 phần trăm và lãi suất 60 ngày là 4,4855 phần trăm, thì chênh lệch giữa hai mức lãi suất đã biết là 0,2613 phần trăm.

Bước 2

Chia kết quả từ Bước 1 cho hiệu số giữa độ dài của hai khoảng thời gian. Ví dụ:sự khác biệt giữa khoảng thời gian 60 ngày và khoảng thời gian 30 ngày là 30 ngày. Chia 0,2613 phần trăm cho 30 ngày và kết quả là 0,00871 phần trăm.

Bước 3

Nhân kết quả từ Bước 2 với hiệu số giữa khoảng thời gian cho lãi suất mong muốn và khoảng thời gian cho lãi suất có khoảng thời gian ngắn nhất. Ví dụ:lãi suất mong muốn là 45 ngày nữa, và lãi suất ngắn nhất được biết là lãi suất 30 ngày. Sự khác biệt giữa 45 ngày và 30 ngày là 15 ngày. 15 nhân với 0,00871 phần trăm bằng 0,13065 phần trăm.

Bước 4

Cộng kết quả từ Bước 3 với lãi suất trong khoảng thời gian ngắn nhất đã biết. Ví dụ, lãi suất trong khoảng thời gian 30 ngày là 4,2242 phần trăm. Tổng của 4,2242 phần trăm và 0,13065 phần trăm là 4,35485 phần trăm. Đây là ước tính nội suy cho lãi suất 45 ngày.

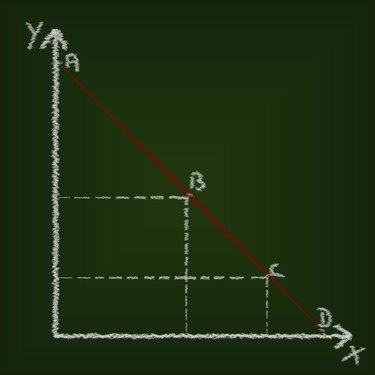
Để đảm bảo rằng bạn đang tuân theo phương trình một cách chính xác, việc vẽ biểu đồ có thể hữu ích. Biểu đồ phải có một trục biểu thị lãi suất, với trục còn lại biểu thị khoảng thời gian. Vẽ đường thẳng qua hai điểm biểu diễn lãi suất đã biết. Nếu lãi suất bạn nội suy nằm ngoài đường này, bạn sẽ biết rằng mình đã mắc lỗi trong quá trình thực hiện.

Nội suy tuyến tính là một ước tính cho lãi suất của một khoảng thời gian cụ thể và nó giả định rằng lãi suất thay đổi trên cơ sở đường thẳng giữa mỗi ngày. Trên thực tế, lãi suất có thể tuân theo "đường cong lợi suất" thay vì đường thẳng. Ước tính sẽ chính xác hơn khi khoảng thời gian giữa các mức lãi suất đã biết mà bạn đang nội suy càng ngắn.