Đầu tiên, điều chắc chắn duy nhất là không có gì chắc chắn cả. Thứ hai, mọi quyết định như một hệ quả đều là vấn đề cân nhắc xác suất. Thứ ba, bất chấp sự không chắc chắn, chúng ta phải quyết định và chúng ta phải hành động. Và cuối cùng, chúng ta cần đánh giá các quyết định không chỉ dựa trên kết quả mà còn cả cách thức đưa ra các quyết định đó.– Robert E. Rubin
Một trong những khía cạnh quan trọng và thách thức nhất của dự báo là xử lý sự không chắc chắn vốn có trong việc kiểm tra tương lai. Đã xây dựng và phổ biến hàng trăm mô hình tài chính và hoạt động cho LBO, gây quỹ khởi nghiệp, ngân sách, M&A và các kế hoạch chiến lược của công ty kể từ năm 2003, tôi đã chứng kiến rất nhiều cách tiếp cận để làm như vậy. Mỗi Giám đốc điều hành, Giám đốc tài chính, thành viên hội đồng quản trị, nhà đầu tư hoặc thành viên ủy ban đầu tư mang đến kinh nghiệm và cách tiếp cận của riêng họ đối với các dự báo tài chính và sự không chắc chắn — bị ảnh hưởng bởi các động lực khác nhau. Thông thường, việc so sánh các kết quả thực tế với các dự báo cung cấp sự đánh giá về mức độ sai lệch giữa các dự báo và kết quả thực tế có thể lớn đến mức nào, và do đó cần hiểu và nhận biết rõ ràng về sự không chắc chắn.
Ban đầu, tôi bắt đầu sử dụng các phân tích kịch bản và độ nhạy để mô hình hóa độ không đảm bảo, và vẫn coi chúng là những công cụ rất hữu ích. Kể từ khi thêm mô phỏng Monte Carlo vào hộp công cụ của tôi vào năm 2010, tôi đã nhận thấy chúng là một công cụ cực kỳ hiệu quả để tinh chỉnh và cải thiện cách bạn nghĩ về rủi ro và xác suất. Tôi đã sử dụng phương pháp này cho mọi thứ, từ việc xây dựng định giá DCF, định giá các quyền chọn mua trong M&A và thảo luận về rủi ro với các bên cho vay để tìm kiếm nguồn tài chính và hướng dẫn phân bổ vốn VC cho các công ty khởi nghiệp. Phương pháp này luôn được các thành viên hội đồng quản trị, các nhà đầu tư và đội ngũ quản lý cấp cao đón nhận. Trong bài viết này, tôi cung cấp hướng dẫn từng bước về cách sử dụng mô phỏng Monte Carlo trong thực tế bằng cách xây dựng mô hình định giá DCF.
Trước khi bắt đầu với nghiên cứu điển hình, hãy xem xét một số cách tiếp cận khác nhau để xử lý sự không chắc chắn. Khái niệm về giá trị kỳ vọng —Trung bình có trọng số xác suất của các dòng tiền trong tất cả các trường hợp có thể xảy ra — là Finance 101. Nhưng các chuyên gia tài chính và những người ra quyết định rộng hơn, có những cách tiếp cận rất khác nhau khi chuyển cái nhìn sâu sắc đơn giản này vào thực tế. Phương pháp tiếp cận có thể bao gồm từ việc đơn giản là không nhận ra hoặc thảo luận về sự không chắc chắn, mặt khác, đến các mô hình và phần mềm phức tạp. Trong một số trường hợp, mọi người cuối cùng dành nhiều thời gian để thảo luận về xác suất hơn là tính toán dòng tiền.
Ngoài việc đơn giản là không giải quyết vấn đề đó, chúng ta hãy xem xét một số cách xử lý sự không chắc chắn trong các dự báo trung hoặc dài hạn. Nhiều người trong số này sẽ quen thuộc với bạn.
| Tạo một kịch bản. Cách tiếp cận này là mặc định cho ngân sách, nhiều công ty khởi nghiệp và thậm chí cả các quyết định đầu tư. Bên cạnh việc không chứa bất kỳ thông tin nào về mức độ không chắc chắn hoặc ghi nhận rằng kết quả có thể khác với dự đoán, nó có thể mơ hồ và được giải thích khác nhau tùy theo các bên liên quan. Một số người có thể hiểu nó là một mục tiêu kéo dài, trong đó kết quả thực tế có nhiều khả năng giảm ngắn hơn là vượt quá. Một số xem nó như một hiệu suất cơ bản với nhiều mặt tăng hơn là giảm. Những người khác có thể xem nó như một "Trường hợp cơ sở" với xác suất 50/50 lên và xuống. Trong một số cách tiếp cận, đặc biệt là đối với các công ty khởi nghiệp, nó rất tham vọng và thất bại hoặc thiếu hụt là kết quả dễ xảy ra hơn cho đến nay, nhưng tỷ lệ chiết khấu cao hơn được sử dụng để giải thích rủi ro. | 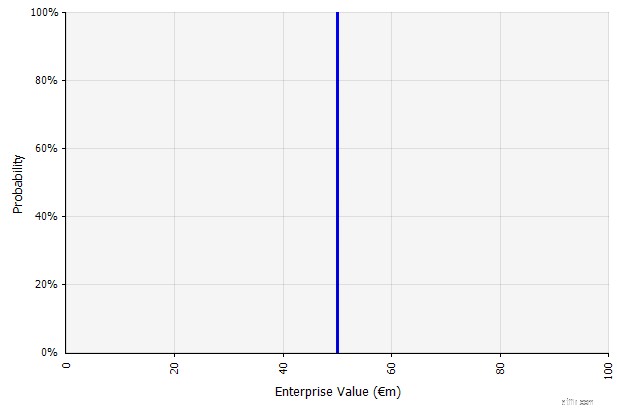 Các yếu tố đầu vào trong dự báo dòng tiền dài hạn theo cách tiếp cận này đều là ước tính điểm, mang lại kết quả ước tính điểm là 50 triệu euro trong ví dụ này, với xác suất ngầm định là 100%. |
| Tạo nhiều tình huống. Cách tiếp cận này thừa nhận rằng thực tế khó có thể diễn ra theo một kế hoạch nhất định.
| 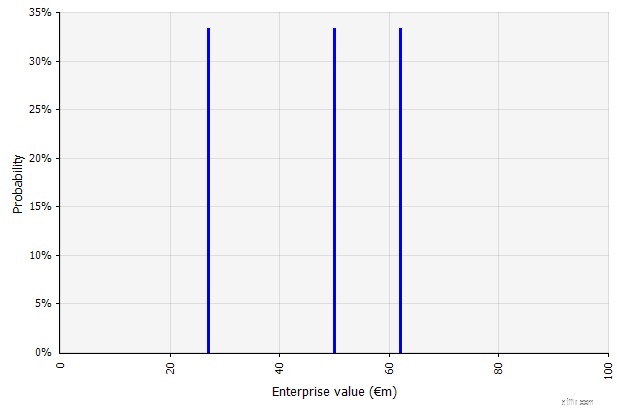 Ba kịch bản khác nhau mang lại ba kết quả khác nhau, ở đây được giả định là có khả năng xảy ra như nhau. Xác suất của các kết quả nằm ngoài kịch bản cao và thấp không được xem xét. |
| Tạo các trường hợp cơ sở, tăng và giảm với các xác suất được công nhận rõ ràng. Nghĩa là, các trường hợp gấu và tăng, ví dụ:xác suất 25% ở mỗi đuôi và ước tính giá trị hợp lý đại diện cho điểm giữa. Một lợi ích hữu ích của việc này từ góc độ quản lý rủi ro là phân tích rõ ràng rủi ro đuôi, tức là, các sự kiện nằm ngoài các kịch bản tăng và giảm. | Hình minh họa từ Sổ tay Định giá Sao mai 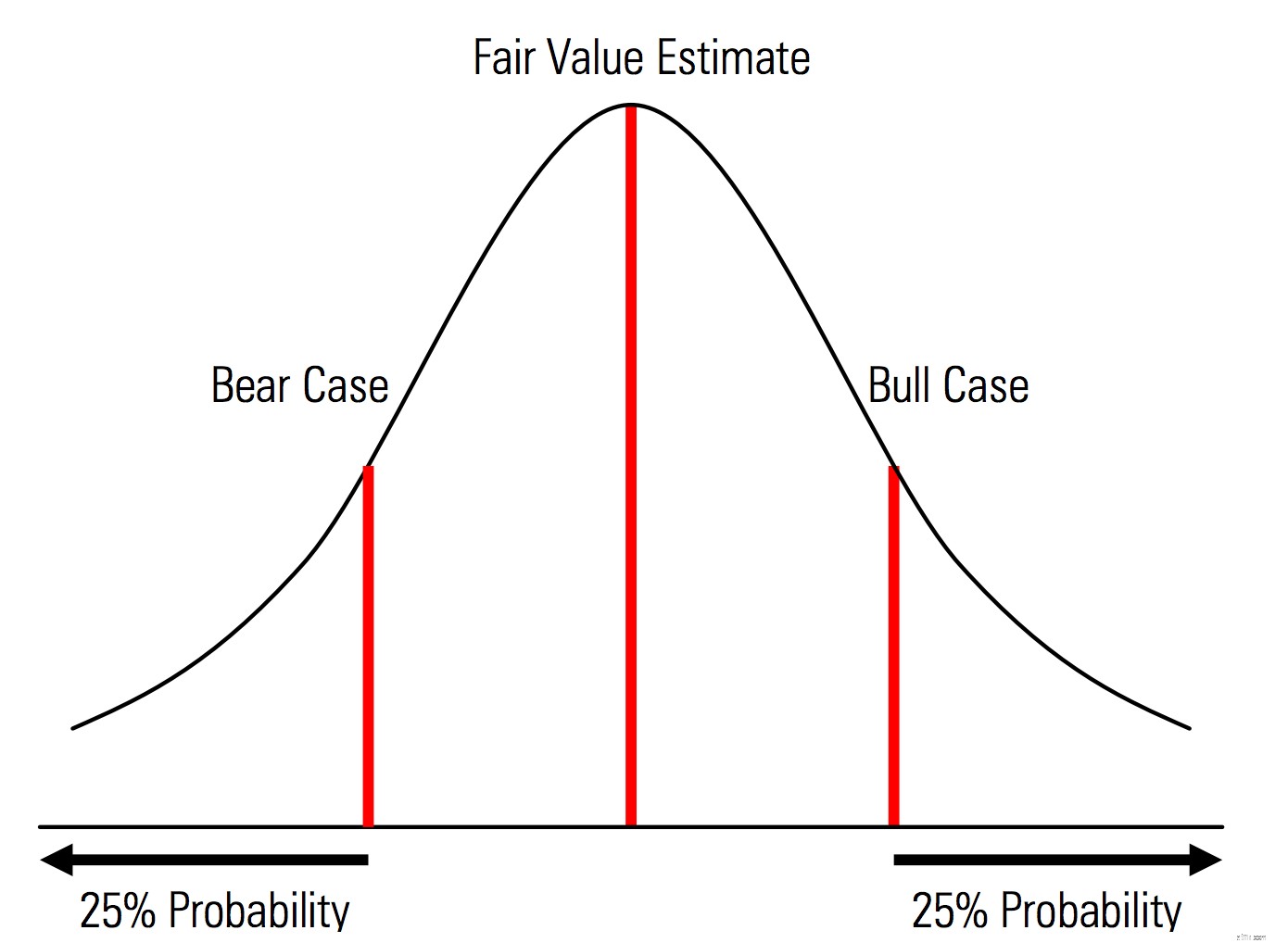 |
| Sử dụng phân phối xác suất và mô phỏng Monte Carlo. Sử dụng phân phối xác suất cho phép bạn lập mô hình và trực quan hóa toàn bộ các kết quả có thể có trong dự báo. Điều này có thể được thực hiện không chỉ ở cấp độ tổng hợp mà còn đối với các đầu vào, giả định và trình điều khiển riêng lẻ chi tiết. Sau đó, các phương pháp Monte Carlo được sử dụng để tính toán các phân phối xác suất kết quả ở mức tổng hợp, cho phép phân tích cách một số biến không chắc chắn đóng góp vào độ không đảm bảo của kết quả tổng thể. Có lẽ quan trọng nhất, phương pháp này buộc mọi người tham gia vào quá trình phân tích và quyết định phải nhận ra một cách rõ ràng tính không chắc chắn vốn có trong dự báo và suy nghĩ về các xác suất. Cũng giống như các phương pháp tiếp cận khác, phương pháp này có những hạn chế của nó, bao gồm nguy cơ sai độ chính xác và dẫn đến sự tự tin quá mức có thể xảy ra khi sử dụng một mô hình phức tạp hơn, và công việc bổ sung cần thiết để chọn các phân bố xác suất phù hợp và ước tính các tham số của chúng, nếu không thì chỉ có các ước tính điểm. đã qua sử dụng. | 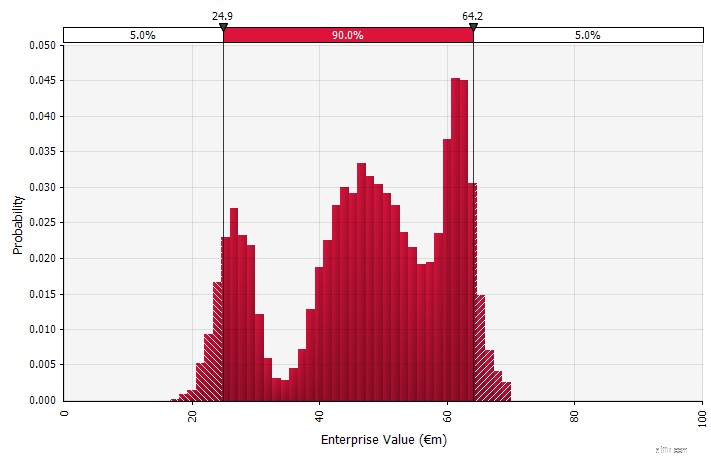 |
Mô phỏng Monte Carlo mô phỏng xác suất của các kết quả khác nhau trong các dự báo và ước tính tài chính. Họ thành danh từ khu vực Monte Carlo ở Monaco, nơi nổi tiếng thế giới với các sòng bạc cao cấp; kết quả ngẫu nhiên là trọng tâm của kỹ thuật, cũng giống như đối với roulette và máy đánh bạc. Mô phỏng Monte Carlo hữu ích trong nhiều lĩnh vực, bao gồm kỹ thuật, quản lý dự án, thăm dò dầu khí và các ngành sử dụng nhiều vốn khác, R&D và bảo hiểm; ở đây, tôi tập trung vào các ứng dụng trong tài chính và kinh doanh.
Trong mô phỏng, các đầu vào không chắc chắn được mô tả bằng cách sử dụng phân bố xác suất, được mô tả bằng các tham số như giá trị trung bình và độ lệch chuẩn. Các yếu tố đầu vào ví dụ trong các dự báo tài chính có thể là bất kỳ thứ gì từ doanh thu và tỷ suất lợi nhuận cho đến một cái gì đó chi tiết hơn, chẳng hạn như giá hàng hóa, chi phí vốn để mở rộng hoặc tỷ giá hối đoái.
Khi một hoặc nhiều đầu vào được mô tả là phân phối xác suất, thì đầu ra cũng trở thành phân phối xác suất. Một máy tính lấy ngẫu nhiên một số từ mỗi phân phối đầu vào và tính toán và lưu kết quả. Điều này được lặp lại hàng trăm, hàng nghìn hoặc hàng chục nghìn lần, mỗi lần được gọi là một lần lặp. Khi được kết hợp với nhau, những lần lặp lại này xấp xỉ phân phối xác suất của kết quả cuối cùng.
Các phân phối đầu vào có thể là liên tục , trong đó giá trị được tạo ngẫu nhiên có thể nhận bất kỳ giá trị nào trong phân phối (ví dụ:phân phối chuẩn) hoặc rời rạc , trong đó các xác suất được gắn với hai hoặc nhiều trường hợp riêng biệt.
Một mô phỏng cũng có thể chứa một hỗn hợp các phân phối của các loại khác nhau. Lấy ví dụ, một dự án R&D dược phẩm với nhiều giai đoạn mà mỗi giai đoạn đều có xác suất thành công hoặc thất bại rời rạc. Điều này có thể được kết hợp với các bản phân phối liên tục mô tả số tiền đầu tư không chắc chắn cần thiết cho từng giai đoạn và doanh thu tiềm năng nếu dự án tạo ra sản phẩm tiếp cận thị trường. Biểu đồ bên dưới cho thấy kết quả từ một mô phỏng như vậy:xác suất ~ 65% mất toàn bộ khoản đầu tư từ 5 triệu euro đến 50 triệu euro (giá trị hiện tại) và ~ 35% xác suất thu được nhiều khả năng nhất trong phạm vi € 100 đến € 250 — thông tin sẽ bị mất nếu các số liệu đầu ra chính như MIRR hoặc NPV được hiển thị dưới dạng ước tính điểm thay vì phân phối xác suất.
Ví dụ Mô phỏng Monte Carlo cho một dự án có một số giai đoạn đi / không và các khoản đầu tư không chắc chắn ở giữa, với giá trị không chắc chắn nếu dự án hoàn thành
Một lý do khiến mô phỏng Monte Carlo không được sử dụng rộng rãi hơn là vì các công cụ tài chính hàng ngày thông thường không hỗ trợ chúng rất tốt. Excel và Google Trang tính giữ một số hoặc kết quả công thức trong mỗi ô và mặc dù chúng có thể xác định phân phối xác suất và tạo số ngẫu nhiên, nhưng việc xây dựng một mô hình tài chính với chức năng Monte Carlo từ đầu là rất cồng kềnh. Và, trong khi nhiều tổ chức tài chính và công ty đầu tư sử dụng mô phỏng Monte Carlo để định giá các công cụ phái sinh, phân tích danh mục đầu tư và hơn thế nữa, các công cụ của họ thường được phát triển nội bộ, độc quyền hoặc cực kỳ đắt tiền - khiến chuyên gia tài chính cá nhân không thể tiếp cận được.
Vì vậy, tôi muốn thu hút sự chú ý đến các plugin Excel như @RISK của Palisade, ModelRisk của Vose và RiskAMP, giúp đơn giản hóa đáng kể việc làm việc với các mô phỏng Monte Carlo và cho phép bạn tích hợp chúng trong các mô hình hiện có của mình. Trong hướng dẫn sau, tôi sẽ sử dụng @RISK.
Chúng ta hãy xem lại một ví dụ đơn giản minh họa các khái niệm chính của mô phỏng Monte Carlo:dự báo dòng tiền trong 5 năm. Trong hướng dẫn này, tôi thiết lập và điền vào một mô hình dòng tiền cơ bản cho mục đích định giá, thay thế dần các yếu tố đầu vào bằng phân phối xác suất và cuối cùng là chạy mô phỏng và phân tích kết quả.
Để bắt đầu, tôi sử dụng một mô hình đơn giản, tập trung vào việc làm nổi bật các đặc điểm chính của việc sử dụng phân phối xác suất. Lưu ý rằng, để bắt đầu, mô hình này không khác bất kỳ mô hình Excel nào khác; các plugin mà tôi đã đề cập ở trên hoạt động với các mô hình và bảng tính hiện có của bạn. Mô hình bên dưới là một phiên bản đơn giản có sẵn với các giả định để tạo thành một kịch bản.
Đầu tiên, chúng ta cần thu thập thông tin cần thiết để đưa ra các giả định của mình, sau đó chúng ta cần chọn các phân phối xác suất chính xác để chèn vào. Điều quan trọng cần lưu ý là nguồn của các yếu tố đầu vào / giả định chính là giống nhau bất kể bạn thực hiện phương pháp tiếp cận nào để xử lý sự không chắc chắn. Thẩm định thương mại, xem xét toàn diện kế hoạch kinh doanh của công ty trong bối cảnh dự kiến phát triển thị trường, xu hướng ngành và động lực cạnh tranh, thường bao gồm ngoại suy từ dữ liệu lịch sử, kết hợp ý kiến chuyên gia, thực hiện nghiên cứu thị trường và phỏng vấn những người tham gia thị trường. Theo kinh nghiệm của tôi, các chuyên gia và những người tham gia thị trường rất vui khi thảo luận về các kịch bản, rủi ro và phạm vi kết quả khác nhau. Tuy nhiên, hầu hết không mô tả rõ ràng các phân phối xác suất.
Bây giờ chúng ta hãy xem xét và thay thế các giá trị đầu vào quan trọng của mình bằng các phân phối xác suất từng cái một, bắt đầu với mức tăng trưởng doanh số ước tính cho năm dự báo đầu tiên (2018). Plugin @RISK dành cho Excel có thể được đánh giá bằng bản dùng thử miễn phí 15 ngày, do đó bạn có thể tải xuống từ trang web Palisade và cài đặt bằng một vài cú nhấp chuột. Với plugin @RISK được bật, hãy chọn ô bạn muốn phân phối và chọn “Xác định phân phối” trong menu.
Sau đó, bạn chọn một từ bảng phân phối xuất hiện. Phần mềm @RISK cung cấp hơn 70 bản phân phối khác nhau để bạn lựa chọn, vì vậy việc lựa chọn một bản phân phối thoạt đầu có vẻ quá sức. Dưới đây là hướng dẫn cho một số ít tôi sử dụng thường xuyên nhất:
| Bình thường. Được xác định bằng giá trị trung bình và độ lệch chuẩn. Đây là một điểm khởi đầu tốt do tính đơn giản của nó và phù hợp như một phần mở rộng cho cách tiếp cận Morningstar, nơi bạn xác định phân phối bao gồm các kịch bản hoặc phạm vi có lẽ đã được xác định cho một đầu vào nhất định, đảm bảo rằng các trường hợp đối xứng xung quanh trường hợp cơ sở và rằng xác suất ở mỗi đuôi có vẻ hợp lý (giả sử 25% như trong ví dụ Morningstar). | 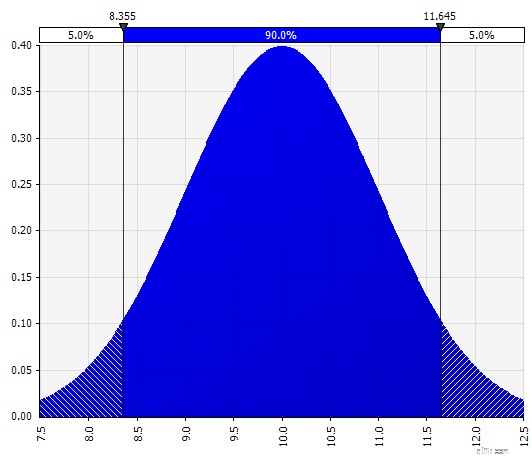 |
| Khoảnh khắc Johnson. Việc chọn điều này cho phép bạn xác định các phân phối lệch và phân phối có đuôi béo hơn hoặc mỏng hơn (về mặt kỹ thuật thêm các thông số lệch và kurtosis). Ở hậu trường, điều này sử dụng một thuật toán để chọn một trong bốn phân phối phản ánh bốn tham số đã chọn, nhưng điều đó là vô hình đối với người dùng --- tất cả những gì chúng ta phải tập trung vào là các tham số.
| 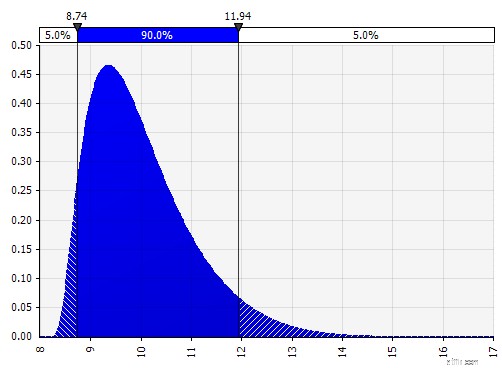 |
| Rời rạc. Trường hợp xác suất được đưa ra cho hai hoặc nhiều giá trị cụ thể. Quay trở lại ví dụ về dự án R&D theo giai đoạn ở phần đầu, xác suất thành công ở mỗi giai đoạn được mô hình hóa dưới dạng phân phối rời rạc nhị phân, với kết quả là 1 đại diện cho thành công và 0 đại diện cho thất bại. | 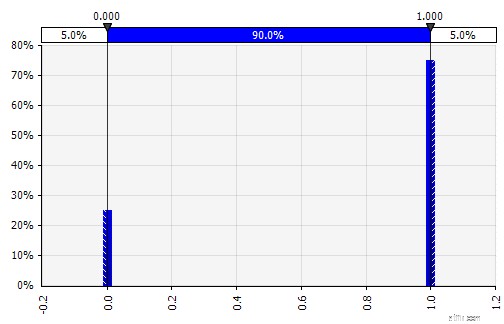 |
| Phù hợp phân phối. Khi bạn có một lượng lớn các điểm dữ liệu lịch sử, chức năng điều chỉnh phân phối rất hữu ích. Ví dụ, điều này không có nghĩa là ba hoặc bốn năm tăng trưởng doanh số lịch sử, mà là dữ liệu chuỗi thời gian như giá hàng hóa, tỷ giá hối đoái hoặc giá thị trường khác, nơi lịch sử có thể cung cấp thông tin hữu ích về xu hướng trong tương lai và mức độ không chắc chắn. | 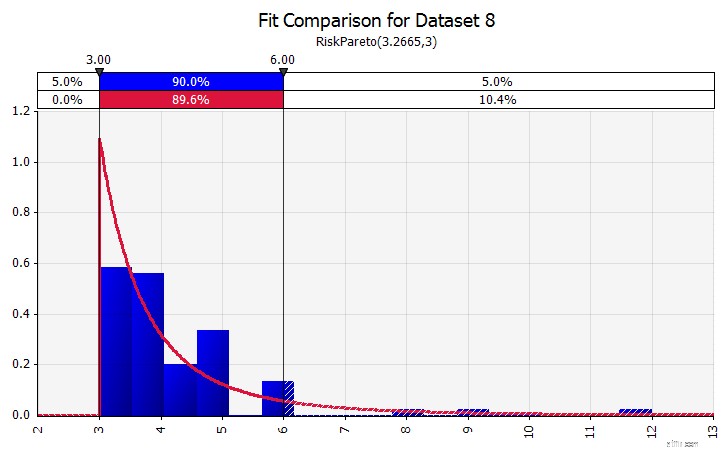 |
| Kết hợp nhiều bản phân phối khác nhau thành một. Để giảm thiểu tác động tiềm tàng của các thành kiến cá nhân, thường là ý kiến hay khi kết hợp đầu vào của các nguồn khác nhau thành một giả định và / hoặc xem xét và thảo luận về các phát hiện. Có các cách tiếp cận khác nhau:
| 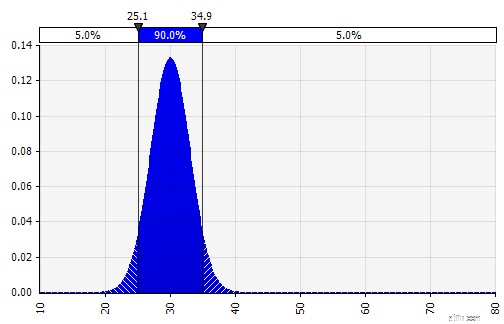 Trọng lượng:20% 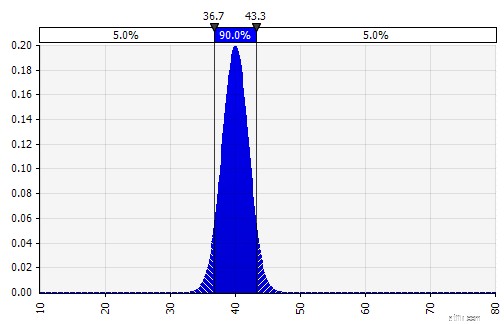 Trọng lượng:20% 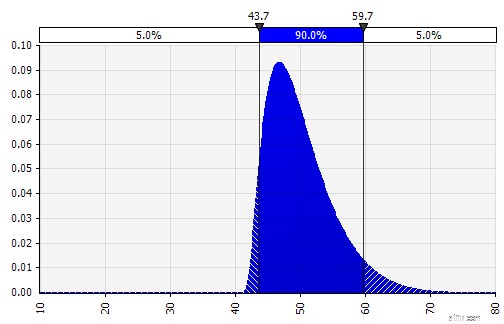 Trọng lượng:60% 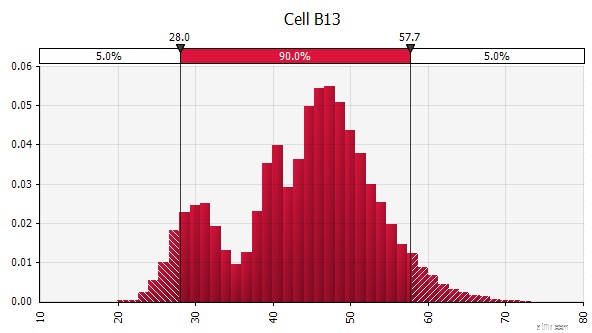 |
| Tự do. Để nhanh chóng minh họa một bản phân phối như một phần của các cuộc thảo luận hoặc nếu bạn cần một bản phân phối khi soạn thảo một mô hình không dễ dàng được tạo từ bảng màu hiện có, chức năng tự do rất hữu ích. Như tên của nó, điều này cho phép bạn vẽ phân bố bằng một công cụ vẽ đơn giản. | 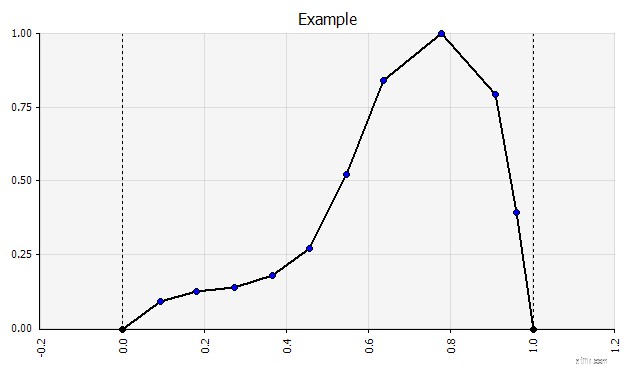 |
Bây giờ chúng ta thấy một hình ảnh trực quan về phân phối, với một vài tham số ở phía bên trái. Các ký hiệu trung bình và độ lệch chuẩn trông quen thuộc. Trong trường hợp phân phối chuẩn, giá trị trung bình sẽ là giá trị trước đây chúng ta đã nhập dưới dạng một giá trị duy nhất trong ô. Dưới đây là phân phối xác suất bán hàng năm 2018 làm ví dụ, với 10% đại diện cho giá trị trung bình. Trong khi mô hình điển hình của bạn sẽ chỉ tập trung vào con số 10% hoặc có các kịch bản “tăng” và “giảm” với mức tăng trưởng tương ứng là 15% và 5%, thì điều này hiện cung cấp thông tin về đầy đủ các kết quả tiềm năng dự kiến.
Phân bổ xác suất của tăng trưởng doanh số bán hàng trong một năm
Một lợi ích của mô phỏng Monte Carlo là kết quả đuôi có xác suất thấp có thể kích hoạt suy nghĩ và thảo luận. Chỉ hiển thị các kịch bản tăng và giảm có thể dẫn đến rủi ro mà những người ra quyết định giải thích đó là giới hạn bên ngoài, loại bỏ bất kỳ kịch bản nào nằm ngoài. Điều này có thể dẫn đến việc ra quyết định sai sót, dẫn đến việc phải đối mặt với những kết quả nằm ngoài khả năng chịu đựng rủi ro của tổ chức hoặc cá nhân. Ngay cả xác suất 5% hoặc 1% cũng có thể không được chấp nhận nếu tình huống được đề cập sẽ gây ra hậu quả thảm khốc.
Với mô hình Monte Carlo, hãy lưu ý đến cách phân bố độ không chắc chắn và xác suất xếp chồng lên nhau, chẳng hạn như theo thời gian. Hãy xem lại một ví dụ. Vì doanh số bán hàng trong mỗi năm phụ thuộc vào sự tăng trưởng của những năm trước, chúng ta có thể hình dung và thấy rằng ước tính doanh số bán hàng năm 2022 của chúng tôi không chắc chắn hơn so với năm 2018 (được hiển thị bằng cách sử dụng độ lệch chuẩn và khoảng tin cậy 95% trong mỗi năm). Để đơn giản hơn, ví dụ dưới đây chỉ rõ mức tăng trưởng trong một năm, 2018 và sau đó áp dụng cùng tốc độ tăng trưởng đó cho từng năm tiếp theo cho đến năm 2022. Một cách tiếp cận khác là có năm phân phối độc lập, mỗi năm một phân phối.
Minh họa cách độ không chắc chắn gia tăng theo thời gian (Mở rộng phân phối kết quả)
Giờ đây, chúng tôi ước tính phân phối xác suất cho biên EBIT trong năm 2018 (được đánh dấu bên dưới) tương tự như cách chúng tôi đã thực hiện để tăng trưởng doanh số.
Ở đây, chúng ta có thể sử dụng hàm tương quan để mô phỏng một tình huống có mối tương quan rõ ràng giữa thị phần tương đối và khả năng sinh lời, phản ánh tính kinh tế theo quy mô. Các kịch bản có tăng trưởng doanh số bán hàng cao hơn so với thị trường và thị phần tương ứng cao hơn tương ứng có thể được mô hình hóa để có mối tương quan thuận với tỷ suất lợi nhuận EBIT cao hơn. Trong những ngành mà tài sản của công ty có tương quan chặt chẽ với một số yếu tố bên ngoài khác, chẳng hạn như giá dầu hoặc tỷ giá hối đoái, việc xác định phân phối cho yếu tố đó và lập mô hình mối tương quan với doanh số và lợi nhuận có thể có ý nghĩa.
Mô hình hóa mối tương quan giữa tăng trưởng doanh số và tỷ suất lợi nhuận
Tùy thuộc vào thời gian có sẵn, quy mô giao dịch và các yếu tố khác, việc xây dựng mô hình hoạt động và nhập các biến không chắc chắn nhất một cách rõ ràng là rất hợp lý. Chúng bao gồm:khối lượng và giá sản phẩm, giá hàng hóa, tỷ giá hối đoái, chi tiết đơn hàng chính, người dùng hoạt động hàng tháng và doanh thu trung bình trên mỗi đơn vị (ARPU). Cũng có thể lập mô hình ngoài các biến số như thời gian phát triển, thời gian đưa ra thị trường hoặc tỷ lệ chấp nhận thị trường.
Bằng cách sử dụng phương pháp đã nêu, giờ đây chúng ta có thể tiếp tục thông qua bảng cân đối kế toán và báo cáo lưu chuyển tiền tệ, đưa vào các giả định và sử dụng phân phối xác suất nếu nó có ý nghĩa.
Một lưu ý về capex:điều này có thể được mô hình hóa theo số tiền tuyệt đối hoặc theo tỷ lệ phần trăm doanh thu, có khả năng kết hợp với các khoản đầu tư từng bước lớn hơn; Ví dụ, một cơ sở sản xuất có thể có một giới hạn công suất rõ ràng và một khoản đầu tư mở rộng lớn hoặc một cơ sở mới cần thiết khi doanh số bán hàng vượt quá ngưỡng. Vì mỗi 1.000 hoặc 10.000 lần lặp sẽ là một phép tính lại hoàn chỉnh của mô hình, nên có thể sử dụng một công thức đơn giản kích hoạt chi phí đầu tư nếu / khi đạt đến một khối lượng nhất định.
Xây dựng mô hình Monte Carlo có một bước bổ sung so với mô hình tài chính tiêu chuẩn:Các ô mà chúng ta muốn đánh giá kết quả cần được chỉ định cụ thể làm ô đầu ra. Phần mềm sẽ lưu kết quả của mỗi lần lặp lại mô phỏng cho các ô đó để chúng ta đánh giá sau khi mô phỏng xong. Tất cả các ô trong toàn bộ mô hình được tính toán lại với mỗi lần lặp, nhưng kết quả của các lần lặp trong các ô khác, không được chỉ định là ô đầu vào hoặc đầu ra, sẽ bị mất và không thể phân tích sau khi mô phỏng kết thúc. Như bạn có thể thấy trong ảnh chụp màn hình bên dưới, chúng tôi chỉ định ô kết quả MIRR là ô đầu ra.
Khi bạn đã xây dựng xong mô hình, đã đến lúc chạy mô phỏng lần đầu tiên bằng cách chỉ cần nhấn “bắt đầu mô phỏng” và đợi trong vài giây.
Kết quả đầu ra được biểu thị dưới dạng xác suất. Trong khi mô hình của chúng tôi trước đây cung cấp cho chúng tôi một giá trị duy nhất cho IRR được sửa đổi, thì giờ đây chúng tôi có thể thấy rõ rằng có một số kết quả tiềm năng xung quanh giá trị đó, với các xác suất khác nhau. Điều này cho phép chúng tôi diễn đạt lại các câu hỏi, chẳng hạn như "Liệu chúng tôi có đạt được tỷ lệ hoàn vốn vượt rào với khoản đầu tư này không?" để "Chúng ta có khả năng đạt hoặc vượt quá tỷ lệ vượt rào của mình như thế nào?" Bạn có thể khám phá xem kết quả nào có nhiều khả năng xảy ra nhất, chẳng hạn như khoảng tin cậy. Hình ảnh trực quan rất hữu ích khi truyền đạt kết quả cho các bên liên quan khác nhau và bạn có thể phủ các kết quả đầu ra từ các giao dịch khác để so sánh trực quan mức độ hấp dẫn và (không) chắc chắn của kết quả hiện tại so với các giao dịch khác (xem bên dưới).
IRR được sửa đổi với Khoảng tin cậy
IRR được sửa đổi với tỷ lệ nhanh
IRR được sửa đổi với các giao dịch khác được phủ lên
Hiểu mức độ không chắc chắn trong kết quả cuối cùng. Nếu chúng ta tạo biểu đồ về sự thay đổi của dòng tiền theo thời gian, tương tự như những gì chúng ta đã làm ban đầu cho hoạt động bán hàng, thì rõ ràng là sự biến đổi của dòng tiền tự do trở nên đáng kể ngay cả với sự không chắc chắn tương đối khiêm tốn trong bán hàng và các yếu tố đầu vào khác mà chúng ta đã mô hình hóa dưới dạng phân phối xác suất , với kết quả dao động từ khoảng 0,5 triệu € đến 5,0 triệu € — hệ số gấp 10 lần — thậm chí chỉ một độ lệch chuẩn so với giá trị trung bình. Đây là kết quả của việc xếp chồng các giả định không chắc chắn lên nhau, một tác động kết hợp cả “chiều dọc” qua các năm và “chiều ngang” trong báo cáo tài chính. Hình ảnh hóa cung cấp thông tin về cả hai dạng không chắc chắn.
Sự thay đổi của dòng tiền tự do so với sự thay đổi của doanh số bán hàng
Phân tích độ nhạy:Giới thiệu biểu đồ lốc xoáy. Một lĩnh vực quan trọng khác là hiểu đầu vào nào có tác động lớn nhất đến kết quả cuối cùng của bạn. Một ví dụ cổ điển là tầm quan trọng của các giả định về tỷ lệ chiết khấu hoặc giá trị cuối cùng thường được đưa ra quá ít trọng số so với dự báo dòng tiền. Một cách phổ biến để xử lý điều này là sử dụng ma trận trong đó bạn đặt một đầu vào chính trên mỗi trục và sau đó tính toán kết quả trong mỗi ô (xem bên dưới). Điều này đặc biệt hữu ích trong các tình huống mà các quyết định xoay quanh một hoặc một vài giả định chính — trong những tình huống “bạn phải tin” này, những người ra quyết định trong (ví dụ) một ủy ban đầu tư hoặc một nhóm quản lý cấp cao có thể có những quan điểm khác nhau về those key assumptions, and a matrix such as the one above allows each one of them to find a result value corresponding to their view, and can decide, vote, or give advice based on that.
Example Sensitivity Analysis Matrix - Enterprise Value as a Function of the Cost of Capital and Year Five Exit Multiple
Enhancing with Monte Carlo simulations. When using Monte Carlo simulations, that approach can be complemented with another:the tornado diagram. This visualization lists the different uncertain inputs and assumptions on the vertical axis and then shows how large the impact of each is on the end result.
Tornado Diagram Showing Sensitivity to Key Inputs
This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.
Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.
Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb
It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.
In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.
The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.
In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.
There are two concepts here and it is important to separate them:one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it:Monte Carlo simulations in spreadsheets.
I don’t use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.
Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.
I spend 98% of my time on 2% probabilities – Lloyd Blankfein
Cách thực hiện nhiệm vụ của người thừa hành di sản
Tại sao tôi ghét Phân tích Monte Carlo và các dự báo tài chính khác
Đừng đặt cược việc nghỉ hưu của bạn trên các mô hình Monte Carlo
Phân tích định tính cổ phiếu là gì? Và làm thế nào để thực hiện nó?
Giải thích:Phân tích PESTLE (Với ví dụ) như thế nào? Cách thực hiện?